Compilers Part 1 Lexical Analysis

2021-03-21

This is part 1 of my notes from the University of Toronto course CSC467: Compilers. This section covers Lexical Analysis, or Tokenizing.

Find part 2 (parsing) here.

Key concepts of lexical analysis:

The first process that occurs in any compiler is lexical analysis, or partitioning the program into tokens. In general, a token object has:

For example:

Identifiers, or variable names, are non-keyword strings that start with a letter. Identifier is the token type, the pattern is defined by "non-keyword strings that start with a letter," the matching substring will be the identifier string itself, there will not be a value, and the line number will be the line of code where the identifier is located (line # is useful for outputting error messages).

Integer literals are simply digits, perhaps with a + or - in front. In this case, the value attribute will be the integer value (stored as an int in the compiler), as opposed to the matching substring (stored as a string in the compiler).

To define these patterns in a systematic way, we use regular expressions.

Regex

A regular expression, or regex, is a systematic way to define search patterns.

Relevant xkcd

Quick cheat sheet:

A|B is union
!A is not
AB is concatenation
A{i} is iteration (A appearing i times)
A* is 0 or more
A+ is 1 or more
A? is 0 or 1 times
^A is head anchor
A$ is tail anchor
(A) is a group, and can be referred to later in the regex as \1 or $1

Some caveats: a regex cannot describe everything (e.g. there is no way to match every palindrome), and there are also evil regex, where compute time can scale exponentially with input length (these occasionally cause high-profile outages).

Finite Automata

Regexes are great, but we need a way to represent them in a computer. To do this we translate a regex into a finite automata. A finite automata is essentially a state machine, with a finite set of states (or nodes), and a bunch of transitions (or edges). There is one starting state, and one or more accepting states. Each transition is associated with an input, except for epsilon-transitions, which are free to take (don't consume input).

Two main types of finite automata: 1. NFA or Non-deterministic Finite Automata. Can have multiple transitions per input per state; can have epsilon-transitions. Can be in multiple states at one time. More compact, easier to generate. 2. DFA or Deterministic Finite Automata. Only one transition per input per state; no epsilon-transitions. Can only be in one state at a time. Faster to execute.

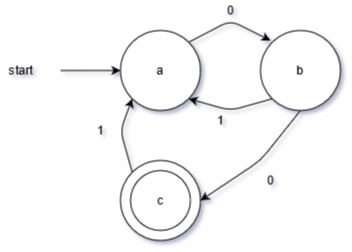
Simple DFA Example

E.g. DFA (above) and NFA (below) which both describe the regex (0|1)*00.

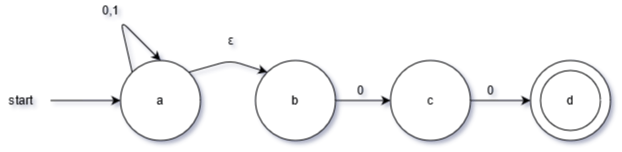
Simple NFA Example

Note that a state is shown by a circle, a matching state is shown by two nested circles, and transitions are given by arrows.

Regex to DFA

For compilers, we define patterns using a regex, which is used to generate an NFA, which gets used to generate a DFA, which finally generates a table that we can use to quickly check for matches.

Regex --> NFA --> DFA --> Table

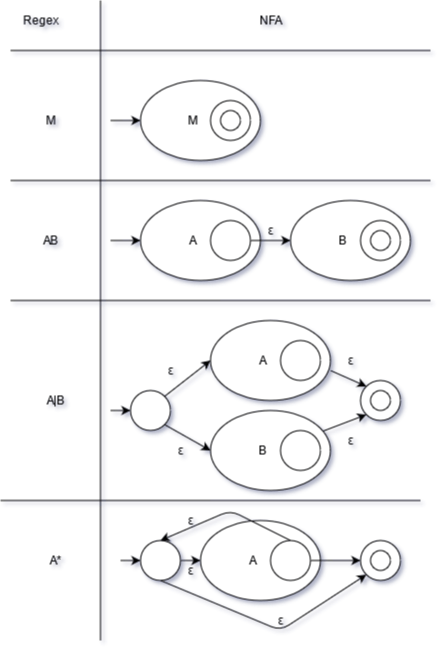
  1. For turning a regex to an NFA, there are a series of rules you can apply, which are summarized in the diagram below.

Regex to NFA Rules

  1. For turning an NFA to a DFA, you merge epsilon-closure states in the NFA (all states reachable by following only epsilon-transitions) into one DFA states. This usually results in more states.

  2. To implement a DFA as a 2D table T: for each transition from state S_i to S_k using input token a, set T[i][a] = k. Then, given a state S_i and the next input a, you can easily find the next state S_k.

Flex

Flex is a lexical tool you can use to tokenize programs. Basically, you define a pattern (with a regex) and a rule action.

e.g. defining a float

DIGIT [0-9]
DIGIT+"."DIGIT* { printf("float: %f\n", atof(yytext)) }

Two important rules flex uses: 1. Longest match rule. If multiple rules match, take the rule that matches the most characters. 2. Priority rule. If 2 rules match with the same number of characters, take the rule listed first.

Errors

Note that the only type of error we can detect at the lexical analysis stage are invalid tokens (e.g. int 0ab; is not a valid identifier in C).